奇数･偶数 (5年算数)

─近似的に答えを求める考え方─

2005.11.26

　円周は、曲線です。
　そのため今まで習った三角形や平行四辺形などとは、違った考え方が要求されます。
　つまり、円の学習では「近似的に答えを求める考え方」を児童にさせていく必要があります。
　アルキメデスの話から、その考え方を紹介したいと思います。

　今から約2300年前に生まれたアルキメデス(古代ギリシア)は、円周率は「３と１０／７１（約3.14085）」と「３と１／７（約3.1426）」のあいだにあると求めました。
　

　下の図を見て下さい。
　　図１は、円周と内接正６角形と外接正６角形です。
　　図２は、円周と内接正１２角形と外接正１２角形です。

　アルキメデスは、円周は、内接正ｎ角形と外接正ｎ角形の外周のあいだの長さであることを利用して、上のような正確な円周率を求めました。
直径４０㎝の円で考えてみます。
ちなみに円周は、１２５．６㎝となります。
＜図１＞ ＜図２＞
外接正６角形の外周 138.6㎝
内接正６角形の外周 120㎝
差 18.6㎝
外接正１２角形の外周 128.62㎝
内接正１２角形の外周 124.23㎝
差 4.39㎝
上の図形の円の直径は、どちらもほぼ同じ長さです。
　アルキメデスは、正６角形→正１２角形→正２４角形→正４８角形→正９６角形とやって円周率を求めました。

　さて、そこで問題です。
　外接正９６角形と内接正９６角形の外周の差は、何㎝だと思いますか？
外接正９６角形 　　　　　　　？㎝
内接正９６角形 　　　　　　　？㎝
差 ？㎝
正解を知りたい場合はここをクリック

　授業では、下の写真のように、アクリル板に緑色とピンク色のひもで貼ることにより、長さの違いを見てはっきりととらえられるようにしておきました（両面テープ使用）。

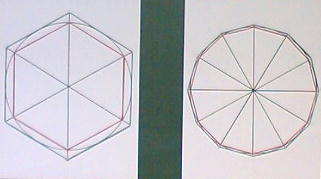内接正６角形外周と内接正１２角形外周→ピンク色のひも
外接正６角形外周と外接正１２角形外周→緑色のひも

この二つの図を見て、気がつくことを発表させました。
　　↓
下の写真は、上のひもをはがして掲示したものです。
左側が正６角形
右側が正１２角形
３本の線のうち、真ん中は円周

　アルキメデスのように円を細かく分けて考えていくほど、限りなく円周率は正確に求めることができます。
　「近似的に答えを求める考え方」は、円の面積の公式を求める際にも使えます。

ホーム